PLOTTING FUNCTION GRAPH USING JAVASCRIPT (Part 1)

Note: Please wait a bit for the math formulas to appear.(I use MathJax.js)

Let consider a spring-mass system with the mass sliding on a horizontal surface. The force of dry friction between the mass and the surface is called Coulomb friction. \[F_{cl} = \mu.m.g\] $\mu$ is the coefficient of friction.
The half period (0.5*T) is the time for the mass to move in one direction from rightmost position to leftmost position or vice versa from extreme left to extreme right.
The period T is the time for the mass to move from the rightmost position to the left and then moving back to the new rightmost position.
We can prove that: \[T = \frac{2\pi}{\omega}\quad\text{and}\quad\omega=\sqrt{\frac{k}{m}}\] The minimum stretch d of spring for oscillation to start ($x_0 > d$): \[k.d = F_{cl}=\mu.m.g\quad\to\quad d = \frac{F_{cl}}{k}\] We can prove that: The loss of amplitude in half period is \[2.d = 2.\frac{\mu.m.g}{k}\] The following is the JPG picture of my web page "sin-small-15.html"
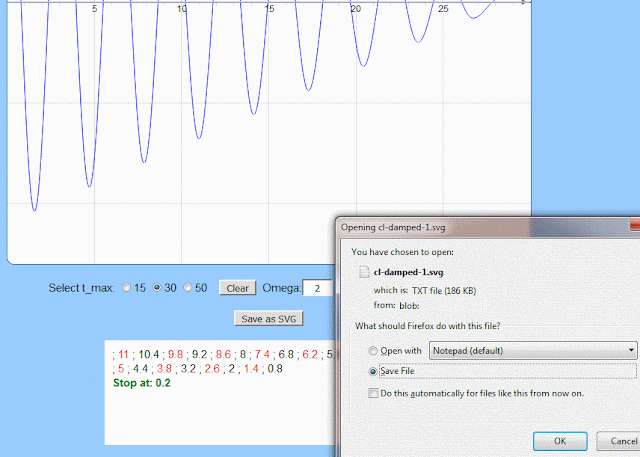
At the top of the page is the oscillating graph of the spring-mass system with
an angular frequency of 2 (rad/s), d = 0.3 (cm)
and when t = 0: x0 = 11 cm (v0 = 0)

To plot a new graph you need to act as the below:
- Click the button "Clear"
- Enter new values for "Omega","x_0" and "d"
- Click the button "Show"

4- HTML and JavaScript Source code

<!DOCTYPE HTML>
<html>
  <head>
  <meta http-equiv="content-type" content="text/html; charset=utf-8">
  <title>Coulomb OSC</title>
<head>
<style>
 body{
 font-family:'Arial';
 font-size:11pt;
 margin:0px; padding:0px;
 background-color:#99CCFF;
 }
 input[type=text]{background-color:white; text-align:center}
 button{background-color:#DDDDDD} 
 </style>
 <link rel="stylesheet" type="text/css" href="http://jsxgraph.uni-bayreuth.de/distrib/jsxgraph.css" />
 <style>
 </style>
 <script type="text/javascript" src="http://jsxgraph.uni-bayreuth.de/distrib/jsxgraphcore.js"></script>
 
 <script src="http://cdn.jsdelivr.net/g/filesaver.js"></script>
 </head>
  
  <body onload="init()">
  <div align=center>
  <h2>COULOMB DAMPED OSCILLATION GRAPH</h2>
  <h3>1- Plotting graph using javascript</h3> 
  <div id="box" class="jxgbox" style="width:700px; height:700px;"></div>
  <br>
  <label for="gender">Select t_max: </label>
    <input type="radio" name="widthRadio" value="15" onclick="init()">15
    <input type="radio" name="widthRadio" value="30" checked onclick="init()">30
    <input type="radio" name="widthRadio" value="50" onclick="init()">50
    &nbsp;&nbsp;
  <button onclick="clr()">Clear</button>&nbsp;
  Omega:<input type=text id="omega" size=3 value=2>&nbsp;
  x_0:<input type=text id="x0" size=4 value=11>&nbsp;
  d:<input type=text id="d" size=4 value=0.3>&nbsp;
  <button onclick="show()">Show</button>
  <br><br>
  <button onclick="saveSVG()">Save as SVG</button>
  <br><br>
  <div id="div1" style="width:420px;height:120px;padding:10px;text-align:left;overflow:auto;background-color:white">
  </div>
  <br>
  </div>
<script>
  wid = 30;
  
  function init(){
      var radios = document.getElementsByName('widthRadio');
      for (var i = 0, length = radios.length; i < length; i++){
          if (radios[i].checked){
              wid = radios[i].value;
              break;
          }
      }
      brd1 = JXG.JSXGraph.initBoard('box', {boundingbox: [0, 13, wid, -13], axis:true});
  }
      
  Pi = Math.PI; nn = 2000; var  f 
  var brd1 = JXG.JSXGraph.initBoard('box', {boundingbox: [0, 13, wid, -13], axis:true});
  
  function show(){
       w = Number(document.getElementById('omega').value);
       x0 = Number(document.getElementById('x0').value);
       d = Number(document.getElementById('d').value);
       for(i= 0; i<nn; i++){
          if(x0-(2*i+1)*d + d > d ){
          
              mm1 = x0-(2*i+1)*d + d;
              mm = Math.round(mm1 * 100) / 100;
              if(i % 2 == 0){mm ='<span style="color:red">'+ mm + '</span>'}
              if((i+1) % 10 == 0 ){mm = mm + '<br>'}
              
              st = document.getElementById('div1').innerHTML;
              document.getElementById('div1').innerHTML = st + '  ;  ' + mm;
              
              f = brd1.createElement('functiongraph',
              [function(x){
                  if(x>i*Pi/w && x <(i+1)*Pi/w){ 
                    return (x0-(2*i+1)*d)*Math.cos(w*x) + Math.pow(-1,i)*d;
                  }else{
                      return 0
                    // break;
                  } 
              }]);
              
          } else{
               mm2 = (x0-(2*i+1)*d)*Math.cos(Pi*(i+2)) + Math.pow(-1,i)*d;
               mm3 = Math.round(mm2 * 100) / 100;
               st = document.getElementById('div1').innerHTML;
               document.getElementById('div1').innerHTML = st + 
               '<br><span style="color:green"><b>Stop at: ' + mm3+'</b></span>';
               break
          }
      }
      var xr = brd1.create('line',[[0,0],[10,0]],{visible:true, strokeColor: "#CCCCCC"});
  }
  
  function saveSVG(){
      var svg = new XMLSerializer().serializeToString(brd1.renderer.svgRoot);
      // alert(svg);
      var blob = new Blob([svg], {type: "text/plain;charset=utf-8"});
      saveAs(blob, "cl-damped-1.svg");
  }
      
  function clr(){  
      brd1 = JXG.JSXGraph.initBoard('box', {boundingbox: [0, 13, wid, -13], axis:true});
      document.getElementById('div1').innerHTML = '';
  }
  
</script>
</body>
</html>

DOWMLOAD 4 files (html, tex, pdf graph, svg graph) - 68 KB
http://www.mediafire.com/file/9ax3q4ufgpiq7ta/damped-oscillation-15.zip

JAVASSCRIPT ON IPAD (to see the list click ← then click ≡ and ⌄)

PLOTTING FUNCTION GRAPH USING JAVASCRIPT (Part 1)

4- HTML and JavaScript Source code

Popular posts from this blog

PHP JQUERY PROXY DEMO

SEARCH FOR PIXABAY PHOTOS

DOWNLOAD pixab-15.html